
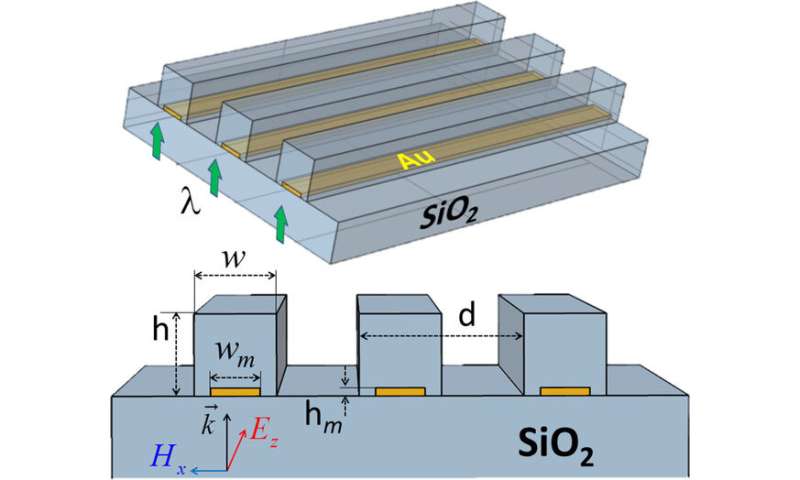
Other phase retrieval schemes require several exposures of the same object, such as ptychography 26 and the recently introduced double-blind Fourier holography (DBFH) 27. Unfortunately, the generation of a well-characterized reference wave can be a difficult, and in some cases infeasible, task. When applicable, Fourier holography techniques 21, 22, 23, 24, 25 offer a single-shot, direct phase reconstruction that avoids the convergence and stagnation issues of AP algorithms. In this case, the phase is mapped to an amplitude modulation, and can be uniquely retrieved by a straightforward calculation. An alternative approach for retrieving the phase is holography, in which the unknown scattered wave is interfered with a known reference wave. Although successful, AP algorithms have certain limitations, in some cases they may stagnate, in particular for complex-valued (phase) objects 20. For decades, phase retrieval relied mainly on non-convex, iterative, alternating projection (AP) algorithms 1, 2. However, retrieval of the phase is a non-convex, challenging computational task, which has been the subject of extensive study 2, 14, 15, 16, 17, 18, 19. In two and three dimensions, with sufficient oversampling, the phase retrieval problem is known to have a unique solution if the object has a finite extent (denoted as its compact support) 12, 13. To reconstruct the object, the Fourier phase has to be retrieved from this diffraction pattern alone. Such ‘diffraction before destruction’ methods 8, 9, 10, 11 are inherently restricted to a single diffraction pattern from every object. These pulses are bright enough to scatter a considerable amount of light from a single molecule, and fast enough to do it long before it starts to dissociate. Recent progress in X-ray sources such as X-ray free-electron lasers (XFELs) has provided ultra-bright X-ray pulses, which are as short as few femtoseconds. Specifically, an extremely promising application is ‘diffraction before destruction’ experiments. Since suitable lenses are not available at the very-short-wavelength (X-ray) regime, retrieval of the Fourier phase is of crucial importance. The fundamental bound on resolution-the diffraction limit-implies that imaging from a distance with subnanometric resolution requires short-wavelength sources. An important branch of applications is high-resolution imaging, the importance of which to physics, material science and biology cannot be overestimated. It has found numerous applications spanning from nature’s smallest scales to the largest: from quantum physics 4, material science 5 and biology 6, to communications and astronomy 7. Reconstructing the phase of a field from intensity measurements is an old and ubiquitous challenge, known as the phase retrieval problem 1, 2, 3. Our scheme alleviates several limitations of current methods, offering a new pathway towards direct reconstruction of complex objects. We establish our method numerically and experimentally in the optical domain and demonstrate a proof-of-principle single-shot coherent diffractive imaging using X-ray free-electron lasers pulses. In our approach, the objects serve as unknown references to one another, reducing the phase problem to a solvable set of linear equations. Here we present a convex scheme for single-shot phase retrieval for two (or more) sufficiently separated objects, demonstrated in two dimensions. Presently, the phase is reconstructed by iterative algorithms, imposing a non-convex computational challenge, or by Fourier holography, requiring a well-characterized reference field. Recent advances in X-ray free-electron lasers allow capturing of the diffraction pattern from a single nanoparticle before it disintegrates, in so-called ‘diffraction before destruction’ experiments. An important application is coherent diffractive imaging.
The non-crystallographic phase problem arises in numerous scientific and technological fields.


 0 kommentar(er)
0 kommentar(er)
